Algebra Explained in Depth: From Pre-Algebra to Linear, Boolean, Binary, and Modern Algebra Systems

Introduction to Algebra

Algebra is one of the most fundamental branches of mathematics, serving as the backbone for advanced mathematical studies, science, engineering, computer science, economics, and everyday problem-solving. Unlike arithmetic, which focuses on numbers, algebra introduces variables, symbols, and generalized relationships that allow us to model real-world situations efficiently.

Whether you are studying pre algebra, algebra 1, algebra 2, linear algebra, or advanced systems like algebra Boole, binary algebra, and magma algebra, algebra helps build logical reasoning and analytical thinking.

In modern education, tools like MathPapa have made learning algebra easier by providing step-by-step solutions, but understanding the core concepts remains essential.

This comprehensive guide explores algebra in detail, covering all major types with formulas and examples.

---

What Is Algebra?

Algebra is a branch of mathematics that uses letters (variables) to represent unknown numbers and describes relationships using equations and expressions.

Basic Components of Algebra

• Variables: Symbols representing unknown values (x, y, z)
• Constants: Fixed numerical values
• Expressions: Combinations of variables and constants
• Equations: Mathematical statements showing equality
• Functions: Rules that assign one output to each input

Example

$$x + 5 = 12$$x+5=12

Solving:$$x = 12 – 5 = 7$$x=12−5=7

---

Pre Algebra: The Foundation of Algebraic Thinking

Pre algebra prepares students for formal algebra by strengthening arithmetic skills and introducing variables.

Key Topics in Pre Algebra

• Integers and whole numbers
• Fractions and decimals
• Ratios and percentages
• Powers and roots
• Simple equations

Example (Pre Algebra Equation)

$$x + 3 = 10$$x+3=10

Solution:$$x = 7$$x=7

Importance of Pre Algebra

Pre algebra builds confidence and ensures students understand number operations before progressing to algebra 1.

---

Algebra 1: Core Concepts and Skills

Algebra 1 introduces formal algebraic techniques used throughout mathematics.

Major Topics in Algebra 1

• Linear equations
• Inequalities
• Polynomials
• Factoring
• Coordinate geometry
• Systems of equations

Linear Equation Example

$$2x + 4 = 12$$2x+4=12

Solution:$$2x = 8 \Rightarrow x = 4$$2x=8⇒x=4

Graphing Linear Equations

Standard form:$$y = mx + c$$y=mx+c

Where:

• $m$m = slope
• $c$c = y-intercept

Example

$$y = 2x + 1$$y=2x+1

This line increases by 2 units for every 1 unit increase in x.

---

Algebra 2 (Algebra2): Advanced Algebraic Methods

Algebra 2 (often written as algebra2) expands on algebra 1 and prepares students for higher mathematics.

Topics Covered in Algebra 2

• Quadratic equations
• Polynomial functions
• Exponents and logarithms
• Rational expressions
• Sequences and series
• Complex numbers

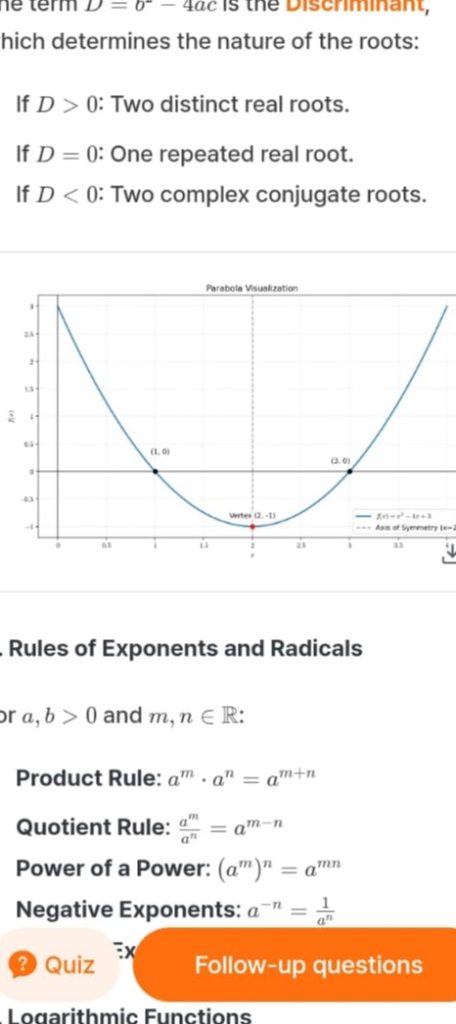
Quadratic Formula

For:$$ax^2 + bx + c = 0$$ax2+bx+c=0

Solution:$$x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}$$x=2a−b±b2−4ac​​

Example

$$x^2 – 5x + 6 = 0$$x2−5x+6=0

Factoring:$$(x – 2)(x – 3) = 0 \Rightarrow x = 2, 3$$(x−2)(x−3)=0⇒x=2,3

---

Linear Algebra: Vectors, Matrices, and Systems

Linear algebra is a powerful branch of algebra used extensively in engineering, computer science, data science, and artificial intelligence.

Key Concepts of Linear Algebra

• Vectors
• Matrices
• Determinants
• Eigenvalues and eigenvectors
• Linear transformations

Matrix Example

$$A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$$A=[13​24​]

Matrix Addition

$$A + B = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix}$$A+B=[13​24​]+[57​68​]=[610​812​]

Applications of Linear Algebra

• Machine learning
• Computer graphics
• Electrical engineering
• Network analysis

---

Boolean Algebra (Algebra Boole)

Algebra Boole, also known as Boolean algebra, is the mathematical foundation of digital electronics and computer logic.

Boolean Values

• 0 (False)
• 1 (True)

Boolean Operations

• AND (·)
• OR (+)
• NOT (¯)

Boolean Laws

• $A + 0 = A$A+0=A
• $A \cdot 1 = A$A⋅1=A
• $A + A = A$A+A=A
• $A \cdot A = A$A⋅A=A

Example

$$A \cdot (A + B) = A$$A⋅(A+B)=A

Applications

• Logic gates
• Computer circuits
• Programming conditions

---

Binary Algebra: Mathematics of Binary Systems

Binary algebra operates using base-2 numbers (0 and 1), forming the foundation of digital computing.

Binary Numbers

• Decimal 5 = Binary 101
• Decimal 10 = Binary 1010

Binary Addition Example

$$101 + 011 = 1000$$101+011=1000

Binary Multiplication

$$101 \times 10 = 1010$$101×10=1010

Uses of Binary Algebra

• Computer processors
• Data storage
• Communication systems

---

Magma Algebra: The Simplest Algebraic Structure

Magma algebra is the most basic algebraic structure in abstract algebra.

Definition

A magma is a set equipped with a single binary operation.

Properties

• Closure only
• No identity required
• No associativity required

Example

Let:$$M = \{1, 2, 3\}$$M={1,2,3}

Define operation:$$a * b = (a + b) \mod 3$$a∗b=(a+b)mod3

This system forms a magma.

Importance of Magma Algebra

• Foundation of group theory
• Used in abstract algebra research

---

Difference Between Algebra Types

Type	Focus	Applications
Pre Algebra	Arithmetic foundations	School mathematics
Algebra 1	Linear equations	Daily problem-solving
Algebra 2	Quadratics, functions	Higher math
Linear Algebra	Matrices, vectors	Engineering, AI
Boolean Algebra	Logic operations	Digital electronics
Binary Algebra	Base-2 arithmetic	Computers
Magma Algebra	Abstract structures	Advanced theory

---

Role of MathPapa in Learning Algebra

MathPapa is a popular online algebra solver that helps students check their solutions.

Advantages

• Step-by-step solutions
• Helpful for algebra 1 and algebra 2
• Quick equation solving

Limitation

MathPapa is a tool, not a replacement for conceptual understanding.

---

Real-World Applications of Algebra

• Finance: Interest and investment calculations
• Physics: Motion and force equations
• Engineering: Circuit analysis
• Computer Science: Algorithms and logic
• Economics: Demand and supply models

---

Tips to Master Algebra

1. Understand concepts, not memorization
2. Practice daily
3. Use graphs and visual aids
4. Solve word problems
5. Verify answers using tools like MathPapa

---

Conclusion

Algebra is more than just equations; it is a universal language of problem-solving. From pre algebra to algebra 1, algebra 2, linear algebra, and advanced systems like algebra Boole, binary algebra, and magma algebra, algebra equips learners with skills essential for academic and professional success.

Mastering algebra opens doors to science, technology, engineering, economics, and beyond. With consistent practice, clear understanding, and the right resources, algebra becomes not only manageable—but enjoyable.